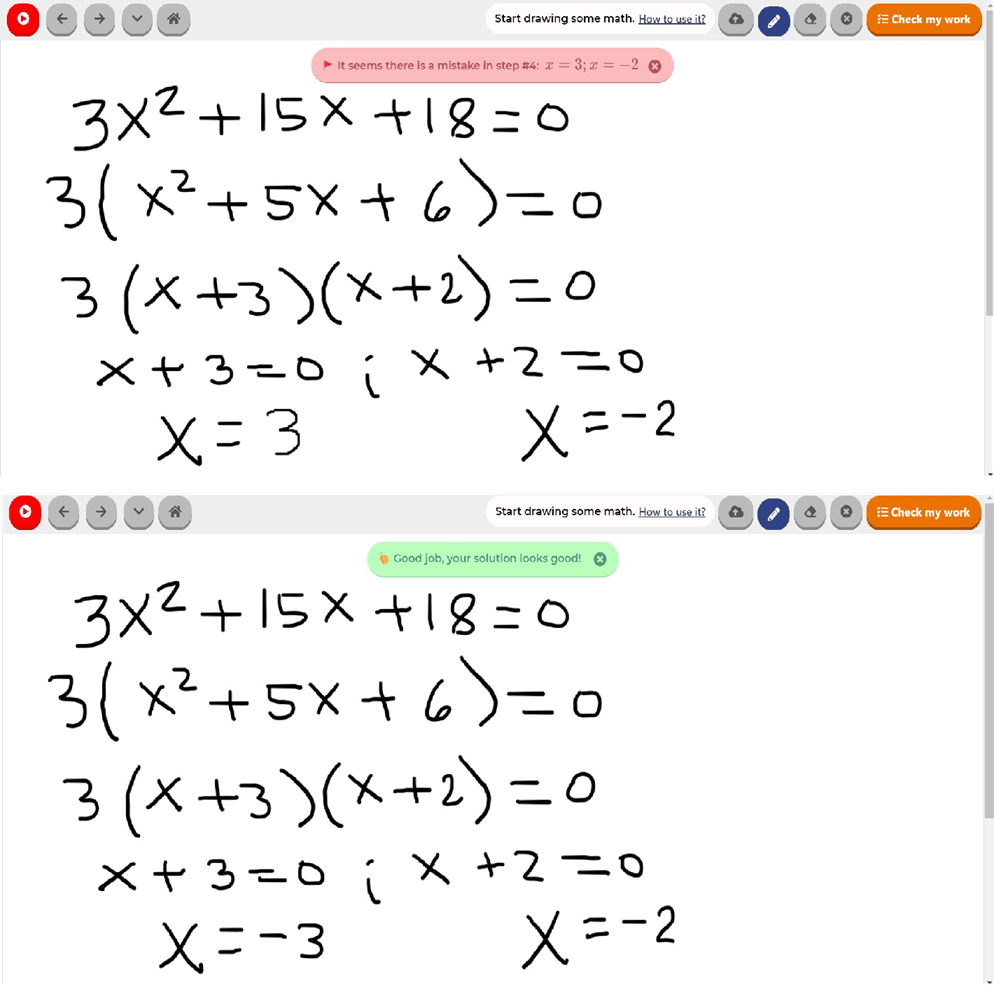
Risposta finale al problema
Soluzione passo-passo
Come posso risolvere questo problema?
- Scegliere un'opzione
- Equazione differenziale esatta
- Equazione differenziale lineare
- Equazione differenziale separabile
- Equazione differenziale omogenea
- Prodotto di binomi con termine comune
- Metodo FOIL
- Per saperne di più...
Dividere tutti i termini dell'equazione differenziale per $x^3$
Applicare la formula: $\frac{a}{a^n}$$=\frac{1}{a^{\left(n-1\right)}}$, dove $a=x$ e $n=3$
Applicare la formula: $\frac{a^m}{a^n}$$=a^{\left(m-n\right)}$, dove $a^n=x^3$, $a^m=x^3$, $a=x$, $a^m/a^n=\frac{x^3}{x^3}$, $m=3$ e $n=3$
Applicare la formula: $x^0$$=1$
Applicare la formula: $\frac{a^m}{a^n}$$=\frac{1}{a^{\left(n-m\right)}}$, dove $a=x$, $m=2$ e $n=3$
Applicare la formula: $a+b$$=a+b$, dove $a=3$, $b=-2$ e $a+b=3-2$
Applicare la formula: $x^1$$=x$
Semplificare
Possiamo identificare che l'equazione differenziale ha la forma: $\frac{dy}{dx} + P(x)\cdot y(x) = Q(x)$, quindi possiamo classificarla come un'equazione differenziale lineare del primo ordine, dove $P(x)=\frac{3}{x}$ e $Q(x)=\frac{1}{x^{2}}$. Per risolvere l'equazione differenziale, il primo passo è quello di trovare il fattore integrante $\mu(x)$
Calcolare l'integrale
Applicare la formula: $\int\frac{n}{x}dx$$=n\ln\left(x\right)+C$, dove $n=3$
Per trovare $\mu(x)$, dobbiamo prima calcolare $\int P(x)dx$
Applicare la formula: $e^{a\ln\left(b\right)}$$=b^a$, dove $a=3$, $b=x$ e $2.718281828459045=e$
Quindi il fattore di integrazione $\mu(x)$ è
Applicare la formula: $a\frac{b}{c}$$=\frac{ba}{c}$, dove $a=x^3$, $b=3y$ e $c=x$
Applicare la formula: $a\frac{b}{c}$$=\frac{ba}{c}$, dove $a=x^3$, $b=1$ e $c=x^{2}$
Applicare la formula: $1x$$=x$, dove $x=x^3$
Applicare la formula: $\frac{a^m}{a^n}$$=a^{\left(m-n\right)}$, dove $a^n=x^{2}$, $a^m=x^3$, $a=x$, $a^m/a^n=\frac{x^3}{x^{2}}$, $m=3$ e $n=2$
Applicare la formula: $\frac{a^n}{a}$$=a^{\left(n-1\right)}$, dove $a^n/a=\frac{3yx^3}{x}$, $a^n=x^3$, $a=x$ e $n=3$
Ora, moltiplicare tutti i termini dell'equazione differenziale per il fattore di integrazione $\mu(x)$ e verificare se è possibile semplificare
Possiamo riconoscere che il lato sinistro dell'equazione differenziale consiste nella derivata del prodotto di $\mu(x)\cdot y(x)$
Integrate entrambi i lati dell'equazione differenziale rispetto a $dx$
Semplificare il lato sinistro dell'equazione differenziale
Applicare la formula: $\int xdx$$=\frac{1}{2}x^2+C$
Poiché l'integrale che stiamo risolvendo è un integrale indefinito, quando finiamo di integrare dobbiamo aggiungere la costante di integrazione $C$
Risolvere l'integrale $\int xdx$ e sostituire il risultato con l'equazione differenziale
Applicare la formula: $a\frac{b}{c}$$=\frac{ba}{c}$, dove $a=x^2$, $b=1$ e $c=2$
Unire tutti i termini in un'unica frazione con $2$ come denominatore comune.
Applicare la formula: $nc$$=cteint$, dove $c=C_0$, $nc=2\cdot C_0$ e $n=2$
Applicare la formula: $xa=\frac{b}{c}$$\to x=\frac{b}{ac}$, dove $a=x^3$, $b=x^2+C_1$, $c=2$ e $x=y$
Trovare la soluzione esplicita dell'equazione differenziale. Dobbiamo isolare la variabile $y$